Machine learning is a powerful tool for neuroscience. Often, we can use tools like regression to get a better understanding how neurons relate to perception and behavior. Here is a short demo of the neural problems that can be solved with non-linear regression. 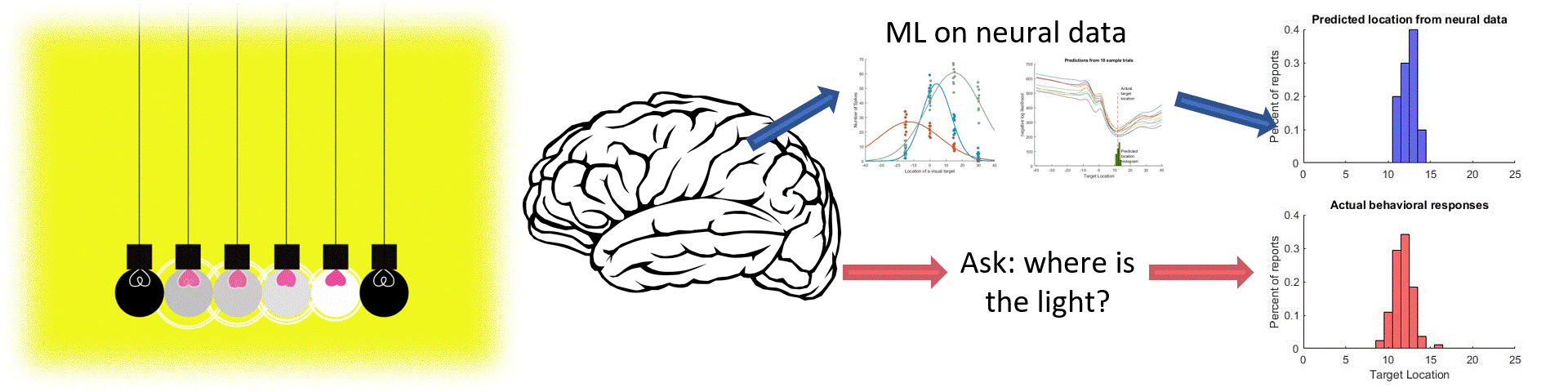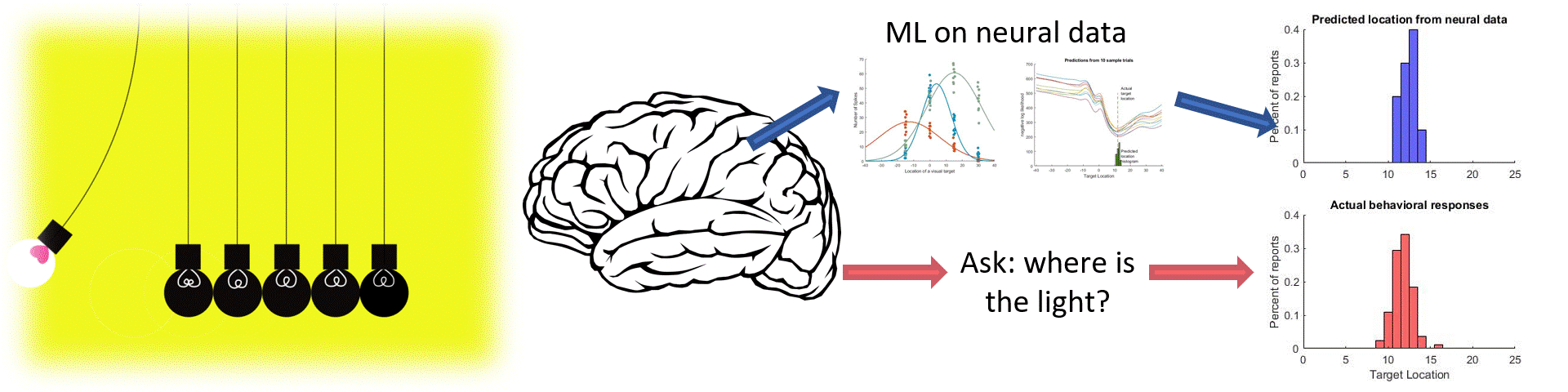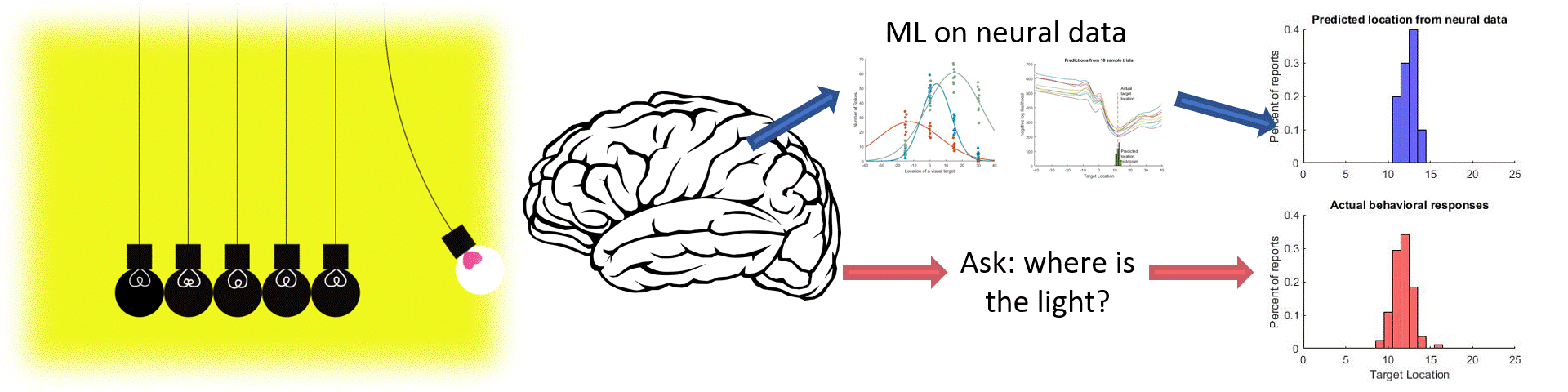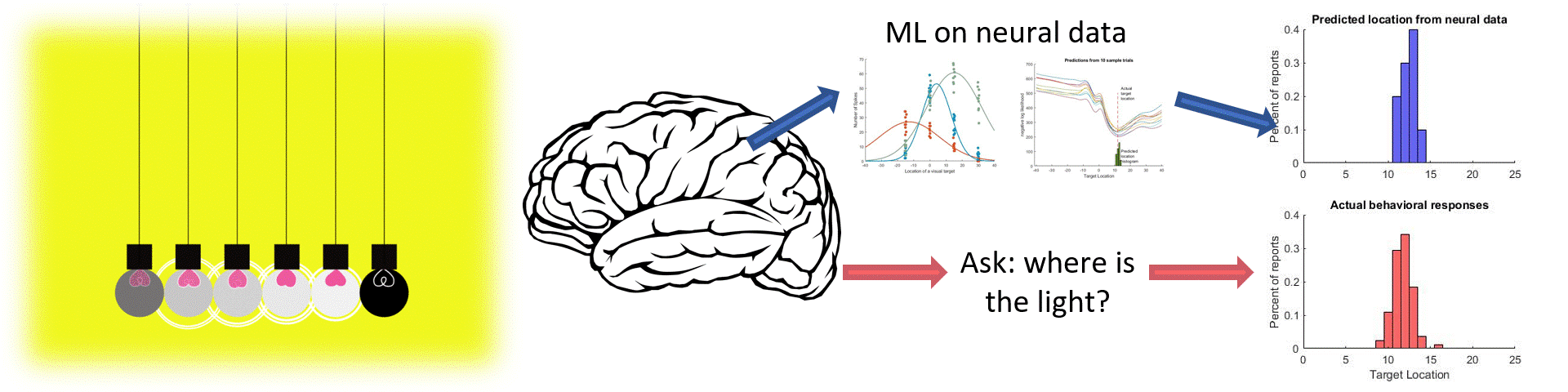
Decoding vision using machine learning approaches
There is a close relationship between machine learning, AI, and systems neuroscience that is often under appreciated (including by neuroscientists). Here I am going to walk through one of the most straightforward, but effective, uses of machine learning for understanding what is going on in the brain: using non-linear regression to relate neural signals to visual stimuli. As you will see, even a relatively simple ML technique is extremely powerful in 'reading out' neural signals, and doing this can be as accurate as simply asking a subject what they saw.
Vision through neurons
Everything you see is the result of neurons in your brain responding to some visual stimulus. Typically, these 'responses' take the form of action potentials or 'spikes', and we can record these spikes using an electrode inserted into the brain. If we record spikes from a single neuron while we show many different types of visual stimulus, we find that some stimuli will generate a lot of spiking activity while others will not. This allows us to find the relationship between the spiking activity of some recorded neuron and the visual stimulus. Once we know this relationship, we can use a tool like regression to go the other direction: take the spiking activity and predict the visual stimulus that is being shown.
For a straightforward example, lets imagine that you are recording a neuron while flashing lights at 4 different locations (here, a negative location means to the left and a positive location means to the right). If you repeat this experiment 10 times for each location, you might get a set of spike counts that looks like the red dots below. There is a lot of noise in the signal (neurons, like many things, have variability that cannot easily be predicted), but there is a clear trend in average spike count as the target location changes. This neuron appears to have a fairly linear relationship between location and spike count. You can use this linear relationship to predict the spike count in between the conditions you tested (a target at the +10 location would be expected to generate around 15 spikes, for instance).
Sometimes neurons have this type of linear relationship, but more commonly they have a more complicated response function. This is often true in other kinds of data, as very few things are truly linearly related. Understanding this relationship between the predictors and your variables of interest is the key to non-linear regression
In many neurons, a very common response function is gaussian tuning. All this means is that there is a specific location where the responses 'peak' and then the number of spikes drop off as you move in either direction, and that this pattern can be roughly described by a gaussian function. This is lucky for us because gaussian functions only have 2 free parameters, and so this only slightly increases the complexity of our model compared to a linear response function. Lets look at two more example cells which more clearly show this peaked behavior.
Here I am plotting two more neurons in addition to the one we had previously. These two new neurons have a clear peak in the data, with green peaking around x=15 and blue peaking around x=5. This highlights another important feature of neurons which is that they often have different relationships between spike count and location. This is critical because having different response functions allows us to resolve potentially confusing situations. For instance, if the blue neuron has a spike count around 25, which could potentially correspond with 2 target locations (x = -10 or x = +15). However, if we also have data from the red and green neurons we can resolve this ambiguity because they have different responses at the two locations in question. If we were to take that trial with 25 spikes in the blue neuron, and see that we also had 60 spikes from the green neuron and 10 spikes from the red neuron, then we would be justified in thinking that the x value was closer to +15 than -10.
And now we are getting to the real power of neurons: combining information from many neurons allows us to get very accurate guesses about target location. This is where non-linear regression finally enters the picture.
Non-linear regression for decoding neural responses
Now that we know the approximate relationship between spike counts and location, we can use this information to turn it around and use it to predict what the stimulus looks like based only on the neural data. To test this we might hold out a few conditions from our training data, and then see if we could predict the locations in each of those conditions based only on the spike counts.
I am going to use a maximum likelihood approach (really minimizing the negative log-likelihood because this is more numerically stable). Given a set of spike counts from the red, green, and blue neurons, can I predict the location that was most likely to generate this set of spikes? Let's start out with just a single condition, x=8. If I have 10 trials worth of held out data, how accurately do I predict the actual target location on those trials?
Here I've plotted the distribution of negative log likelihood (colored lines) for each of the 10 new trials. The lower this value, the more likely it is that the stimulus is at that location. Extracting the most likely location for each trial (green bars) shows that they cluster pretty close to the actual location. There is some variability here, which is expected (we are doing this with just 3 neurons after all!), but clearly there is a lot of predictive power here. Of course this has all been theory up to this point, so how does this work with actual neural data?
Predicting target location from neural data
Now that we've gone through the theory, lets see how this works in practice. Here I've included a sample dataset which includes spike counts from around 9000 total trials across 73 different neurons. This includes 10 different visual target locations which span from -30 to +30 (measured in degrees, but the units don't matter here). I'm going to follow the same procedure as I did with the synthesized data. First, checking the relationship between spike count and target location it seems like gaussian response functions will be a better choice than linear again.
Rather than synthesizing some new hypothetical data, I'm going to use a leave one out strategy to validate this model. Essentially I want to generate a bunch of 'held out' trials to test, while using the remaining data to fit the model.
Just like before, I'm plotting the nll curves for 10 dfferent trials as well as the histogram of 'most likely locations' based on those nll curves. As you can see this regression is doing an excellent job of picking the correct location, as almost all of the predicted locations are within 1 degree of the actual location! This is a very good match for what the subjects are actually percieving, which I can tell because I also collected behavioral data on this task where subjects reported (by making an eye movement) where the target was located. Here I can directly compare the location predicted by the neural data with the actual responses given in the same trials. Not only is there a ton of overlap between the distributions, the neurally predicted reports are actually more precise!
Quantifying model performance
Just looking at plots is one thing, but it would be better to quantify the model performance in a way that is more objective. The best way to do this for this kind of model is just to compute the pearson correlation between the predicted and actual locations for many trials.
The R^2 value here indicates the percentage of variance that is captured by our predictions across all conditions. A Value greater than 0.90 is extremely good, and indicates that we are able to essentially perfectly predict the response location based on the neural response. Hopefully this isn't surprising, because I already knew ahead of time that these neurons were highly related to visual information. But you can imagine applying this approach to different neurons, recording from different regions and perhaps with different tasks, and you will start to appreciate how these tools can be used to learn something new about the way the brain encodes information.
Summary and conclusions
This has mostly been a working exercise for me to ground the relationship between theory and results in my own work. All of the different pieces I've shown here (gaussian response functions, maximum likelihood regression, and leave-one-out decoding) have been well demonstrated in neuroscience, and I chose them because they offer a very straightforward story to understand how these concepts tie together. It was also easy to present this story so simply because the specific neural data I chose has a very nice and clean relationship with the parameter of interest (visual target location). Of course our brains are much more complicated than I have suggested here, and are capable of processing much more complicated features. Characterizing the relationships between complex features and noisy neural data is a huge field in itself, and it becoming increasingly intertwined with advanced machine learning principles( here is a great review if you are interested in seeing the state of the art in this area).
Still, I hope that this page has been useful for getting a preview of the utility and power of even straightforward machine learning techniques for understanding the complex inner workings of the brain.
